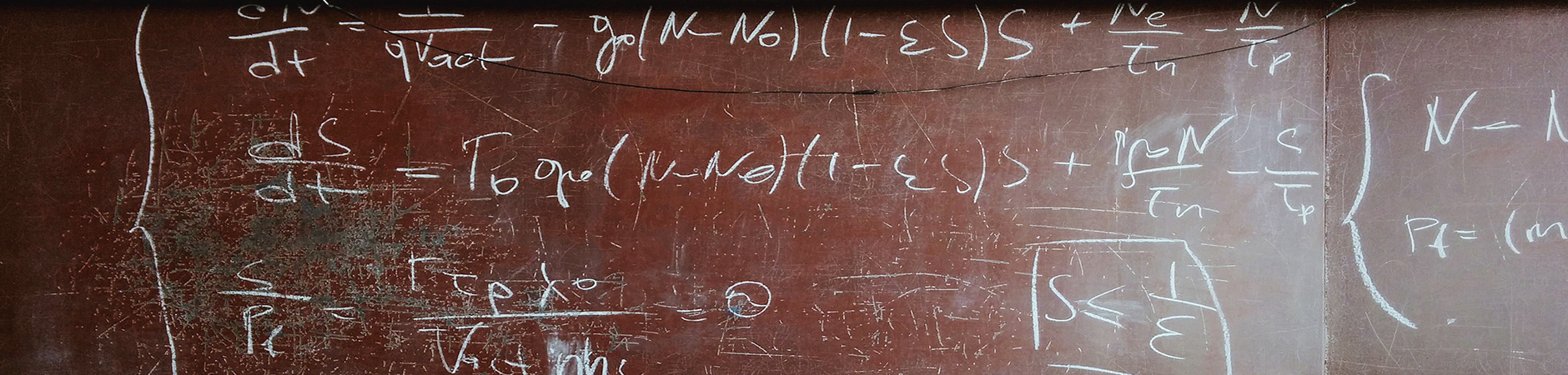
Die Forschung in der Mathematischen Physik in Heidelberg findet an einer Vielzahl von Schnittstellen zwischen den beiden Disziplinen statt und reicht von der Analyse der funktionalen Renormierung und der statistischen Mechanik bis hin zu Anwendungen von Ideen aus der Quantenfeldtheorie in der Topologie und der algebraischen Geometrie. Unser Ziel ist es, sowohl mathematische Theorien zu entwickeln, die von physikalischen Überlegungen inspiriert sind, als auch relevante physikalische Phänomene mathematisch rigoros zu behandeln.
Die fruchtbare Interaktion von Mathematik und Physik ist das Herzstück des Exzellenzclusters STRUCTURES an der Universität Heidelberg.
Vielteilchenphysik: Die Aktivitäten konzentrieren sich auf Vielteilchentheorie, Quantenfeldtheorie und statistische Mechanik. Ein Hauptinteresse gilt der mathematischen Konstruktion von korrelierten Fermentmodellen mit Hilfe von Mehrskalenmethoden, mit Anwendungen in der Theorie der unkonventionellen Supraleitung und anderen symmetriegebrochenen Phasen der Materie.
Zufällige Tensoren und Feldtheorie: Die Aktivitäten konzentrieren sich auf Vielteilchentheorie, Quantenfeldtheorie und statistische Mechanik. Ein Hauptinteresse gilt der mathematischen Konstruktion von korrelierten Fermentmodellen mit Hilfe von Multiskalenmethoden, mit Anwendungen in der Theorie der unkonventionellen Supraleitung und anderer symmetriegebrochener Phasen der Materie. (Gruppe: Prof. Razvan Gurau)
Die Aktivitäten ergeben sich aus der Wechselwirkung zwischen Geometrie und Hochenergiephysik, die seit den 1980er Jahren in der Stringtheorie entstanden ist. Die Forschung stützt sich auf supersymmetrische und topologische Feldtheorien und Supergravitation. Ein zentrales Thema ist die Spiegelsymmetrie in ihren verschiedenen Formulierungen und die mathematische Theorie der BPS-Invarianten.
Ein weiteres zentrales Thema ist die Geometrie, die der so genannten Stringtheorie-Landschaft zugrunde liegt - einer extrem großen Menge von Lösungen, von denen eine möglicherweise unser Universum beschreibt.